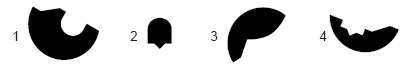|
Задачи международного конкурса Кенгуру Ответы и решения Готовимся к Кенгуру 2010, 3-4 классы 1. Если за каждую гласную букву начислять 2 балла, а за каждую согласную начислять 1 балл, сколько баллов будет начислено за слово КЕНГУРЯТА?
3. Самое маленькое число, которое делится на 10 и на 4, равно 4. Павел в два раза старше Петра, Петр в 3 раза старше Якова, а Якову 4 года. Сколько лет Павлу? 5. Какие фигурки надо взять, чтобы из них можно было составить круг? 6. Какое из этих чисел станет в два раза больше, чем 45, если от него отнять 50? 7. На одной чашке весов лежит 15 слив и 4 яблока, а на другой — 10 слив и 5 яблок. Весы находятся в равновесии. Тогда одно яблоко весит столько же, сколько 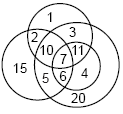 8. Какое число находится во всех четырех кругах? 9. В числе 65834 убрали одну цифру так, чтобы получившееся четы9.
рехзначное число было самым большим из возможных. Тогда сумма цифр этого нового числа равна 10. Два мальчика играют в теннис до четырех побед. Какое самое боль10.
шое число игр может быть сыграно, если ничьих в этом соревновании не бывает? 11. Сколько получится десятков, если два десятка умножить на три десятка? 12. Том поехал к своему другу на велосипеде. Он едет со скоростью 12 км/час и после каждого часа движения отдыхает 15 минут. Том выехал из дома в 8 часов утра и приехал к другу в 11 часов утра. Какое расстояние он проехал? 13. Оловянных солдатиков построили на столе прямоугольником. Перед самым ярким солдатиком в той же колонке стоит 3 солдатика, позади него — 5 солдатиков. Слева от него в том же ряду стоит 6 солдатиков, а справа — 4 солдатика. Сколько всего солдатиков? 14. Вася сложил первые 10 чисел, которые записываются одними едини14.
цами. Какой цифры нет в полученном числе? 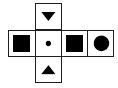 15. Какой кубик мог получиться из развертки? 16. В каждой из двух корзин по три котенка, а еще в четырех корзинах по одному котенку. Что нужно сделать, чтобы котят можно было посадить
по два в каждую корзину и пустых корзин не осталось? 17. Мари было дано задание разделить некоторое число на 4. По ошибке вместо деления она выполнила вычитание и в результате получила число 48. А какой результат должен был получиться? 18. Электронные часы Билла неисправны: иногда они показывают 8 вместо
0, а иногда — 0 вместо 8. Сколько существует моментов в сутках, когда эти часы могут показать ? 19. У Маши было 4 синих шарика и 1 красный. На каждом шарике был свой рисунок: дракон, бабочка, утенок, тигренок и кенгуру. Все шарики улетели. 20. Сколько двузначных четных чисел остаются двузначными четными числами после перестановки своих цифр? 21. ва мальчика хотели купить одинаковые тетрадки, но оказалось, что одному из них не хватает 24 рублей, а другому не хватает 2 рублей. Тогда они решили купить одну тетрадку на двоих, но денег все равно не хватило. Сколько стоила тетрадка, если у каждого мальчика целое число рублей (не меньше, чем 1 рубль), и цена тетрадки — целое число рублей? 22. В январе некоторого года было ровно 4 вторника и 4 субботы. Какой день недели был девятого января? 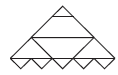 23. Сколько треугольников на картинке? 24. В записи *60 + 18* + 2*3 = *5* нужно все значки * заменить цифрами
1, 3, 5, 7, 8 так, чтобы получить верное равенство. Использовать
каждую цифру можно только один раз. Какое из следующих чисел стоит в правой части этого равенства? 25. На острове Чунга-Чанга используются монеты по 6 и по 7 чангов. Какую самую большую сумму нельзя заплатить такими монетами без сдачи? 26. Алеша и Сережа живут в одном доме, на каждом этаже в каждом подъезде которого расположено по 5 квартир. Алеша живет на четвертом
этаже в квартире номер 79, а Сережа живет в квартире номер 157 на втором этаже. Сколько этажей в доме? |
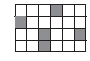2. Сколько белых квадратиков надо перекрасить в серый цвет, чтобы серых клеток было ровно вдвое меньше белых?
|
